CRUSH:受控的、可扩展的数据副本分散存储方案(Part 3)
** 以下内容为翻译
** 原文及版权声明:http://ssrc.ucsc.edu/Papers/weil-sc06.pdf
** 翻译:softrank.net@gmail.com
** 转载请保留以上信息
** 欢迎各位游客指正翻译中的错误,或提出建议
CRUSH:受控的、可扩展的数据副本分散存储方案
作者:Sage A. Weil Scott A. Brandt Ethan L. Miller Carlos Maltzahn
美国加州大学圣克鲁兹分校存储系统研究中心
{sage, scott, elm, carlosm}@cs.ucsc.edu
3.2 副本位置策略
CRUSH的设计使数据得以均匀地分布在带权重的设备上,在统计意义上保持了存储和设备带宽的均衡使用。副本在树状结构中放置的位置对于数据安全性也有着关键性的影响。通过对于系统本质物理结构的映射,CRUSH能够建模,从而定位潜在的相关设备故障源。典型的故障源包括物理位置上接近、共享电源、共享网络。通过将这些信息编码到Cluster Map中,CRUSH的位置策略能够将对象副本分隔到不同的故障域中,同时维持预期的数据分布形式。例如,为了应对出现并发故障的可能性,也许会需要确保数据副本在不同机架、不同机柜、不同电源、不同控制器、不同物理位置的设备上。
CRUSH可以被用于不同的数据副本策略和不同的硬件配置下,为了适应这样的多样性场景的需求,CRUSH为其使用的每个副本策略或分布策略定义Placement Rule,以保证系统或管理员可以确切地指定数据副本如何定位。例如,某人可能设定了某种规则,在某两个目标上使用双重镜像,在某三个设备上使用三重镜像,在某六个存储设备上使用RAID-4等等[注释1:尽管可以用各种各样的数据冗余机制,我们为了简化问题只讨论以副本形式存放的数据对象,也不损失任何的通用性]。
每条规则包含用户简单执行环境的用于树状结构的指令序列,这个运行环境可以用[算法1]中的伪代码来描述。CRUSH算法的输入参数x通常是对象的名称或者其他标识符,比如将被存放在同一个设备上的一组对象的标识符。take(a)操作从层次结构中选中一个项目(往往是一个桶),并将其赋予 ,
, 将作为后续操作的输入。select(n,t)操作对
将作为后续操作的输入。select(n,t)操作对 中的每一个元素i进行迭代,选择n个以i节点为根的子树下具有t类型的项。存储设备都有一个已知的、确定的类型,系统中的每个桶有一个类型字段用于区分不同类型的桶(例如,某些代表“rows”,有些代表“cabinets”)。对
中的每一个元素i进行迭代,选择n个以i节点为根的子树下具有t类型的项。存储设备都有一个已知的、确定的类型,系统中的每个桶有一个类型字段用于区分不同类型的桶(例如,某些代表“rows”,有些代表“cabinets”)。对 中的每一个元素i,select(n,t)操作对于1到n之间的每一个数r被迭代调用,n是请求的项数,操作将递归向下经过任何中间节点的桶,用c(r,x)函数(在章节3.4中为每种类型的桶分别定义)伪随机地在每个桶中选中一个被嵌套的项目,直到找到了满足要求类型t的项。结果的
中的每一个元素i,select(n,t)操作对于1到n之间的每一个数r被迭代调用,n是请求的项数,操作将递归向下经过任何中间节点的桶,用c(r,x)函数(在章节3.4中为每种类型的桶分别定义)伪随机地在每个桶中选中一个被嵌套的项目,直到找到了满足要求类型t的项。结果的 个项,被放回到输入变量
个项,被放回到输入变量 ,可以作为后续的select(n,t)操作的输入参数,也可以通过emit操作将其移入结果向量。
,可以作为后续的select(n,t)操作的输入参数,也可以通过emit操作将其移入结果向量。
 ,
, 将作为后续操作的输入。select(n,t)操作对
将作为后续操作的输入。select(n,t)操作对 中的每一个元素i进行迭代,选择n个以i节点为根的子树下具有t类型的项。存储设备都有一个已知的、确定的类型,系统中的每个桶有一个类型字段用于区分不同类型的桶(例如,某些代表“rows”,有些代表“cabinets”)。对
中的每一个元素i进行迭代,选择n个以i节点为根的子树下具有t类型的项。存储设备都有一个已知的、确定的类型,系统中的每个桶有一个类型字段用于区分不同类型的桶(例如,某些代表“rows”,有些代表“cabinets”)。对 中的每一个元素i,select(n,t)操作对于1到n之间的每一个数r被迭代调用,n是请求的项数,操作将递归向下经过任何中间节点的桶,用c(r,x)函数(在章节3.4中为每种类型的桶分别定义)伪随机地在每个桶中选中一个被嵌套的项目,直到找到了满足要求类型t的项。结果的
中的每一个元素i,select(n,t)操作对于1到n之间的每一个数r被迭代调用,n是请求的项数,操作将递归向下经过任何中间节点的桶,用c(r,x)函数(在章节3.4中为每种类型的桶分别定义)伪随机地在每个桶中选中一个被嵌套的项目,直到找到了满足要求类型t的项。结果的 个项,被放回到输入变量
个项,被放回到输入变量 ,可以作为后续的select(n,t)操作的输入参数,也可以通过emit操作将其移入结果向量。
,可以作为后续的select(n,t)操作的输入参数,也可以通过emit操作将其移入结果向量。
举例说明,[表1]中定义的规则从[图1]中层次结构的root开始,通过第一次select(1,row)操作选中了一个类型为“row”的桶(它选中了row2)。后续的select(3,cabinet)操作在之前选择的row2下面选择了三个各不相同的cabinet(cab21、cab23、cab24),最后一次select(1,disk)在三个cabinet桶之间进行了迭代,对每个cabinet桶在其子树中各选择了1个disk。结果就是分散在3个cabinet中的3个disk,但都在同一个row中。这种方式使得副本能够被同时分发到指定类型(例如row、cabinet、shelf)的设备上,这对提升可靠性与性能都很有帮助。规则包含多个take、emit块,使存储目标可以从不同的存储池中被显式选取出来,在存在远程副本的场景下(某一个副本被存放在远程站点)或者分层架构中(例如高速的近线存储搭配低速大容量阵列)也许会被采用。
[图1:某四级集群映射层次结构的部分视图,包含row、cabinet、shelf和disk。粗体字标出的表示在[表1]中描述的Placement Rules和假想的映射关系中,被每次select操作选中的项。]
| 动作序列 |
结果 |
|---|---|
| take(root) | root |
| select(1,row) | row2 |
| select(3,cabinet) | cab21 cab23 cab24 |
| select(1,disk) | disk2107 disk2313 disk 2437 |
| emit |
[表1:一条简单的规则,将三个副本分发到同一个row的三个不同的cabinet中。]

[算法1:CRUSH确定对象x的存放位置]
3.2.1 冲突、故障和过载
select(n,t)操作可能为了定位n个各不相同的t类型的项而从起点开始向下遍历而经过许多层,递归过程的次数由r=1,...,n确定,n是选择的副本个数。处理过程中,CRUSH可能会由于下面三个不同的原因而用修改过的输入r'来拒绝并重选项:某个项已经在当前的集合中了(发生了冲突,select(n,t)的结果必须是各不相同的);有一个设备失效了;有一个设备过载了。失效或过载的设备会在Cluster Map中进行相应的标记,但为了避免不必要的数据移动,不会从层次结构中移除它们。CRUSH通过根据Cluster Map中指定的概率伪随机地拒绝选择过载设备,来选择性地转移此过载设备上的少部分数据,这个概率则是与报告的过载情况有关的。对于失效或过载的设备,CRUSH通过重新启动select(n,t)开始部分的递归过程(详见[算法1第11行]),均匀地在存储集群中重新分布这些项。而对于冲突的情况,则在递归内层使用r'替换r来进行局部搜索(详见[算法1第14行]),不至于在那些很可能发生冲突的子树中(例如,桶的容量小于n)改变总体的数据分布。
3.2.2 副本排序
与奇偶校验码、擦除码相比,副本方式在存储位置要求上有些许的不同。在主拷贝副本模式中,发生故障时让之前的副本目标(已经有数据的一份拷贝)成为新的主拷贝是可取的。在这种情况下,CRUSH可以通过用r'=r+f进行重选,来使用“前n个”合适的目标,f是当前select(n,t)操作中确定放置位置失败的次数(详见[算法1第16行])。而对于奇偶校验码或者擦除码模式,CRUSH算法输出的存储设备的顺序就至关重要了,因为每个目标都存放了数据对象的不同比特位。特别地,当某个存储设备发生故障时,它需要在CRUSH的输出列表 的对应位置上被替换,其他列表中的设备要维持位置不变(位置就是指在
的对应位置上被替换,其他列表中的设备要维持位置不变(位置就是指在 的对应位置,详见[图2])。在这种情况下,CRUSH通过
的对应位置,详见[图2])。在这种情况下,CRUSH通过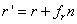 进行重选,其中
进行重选,其中 是第r此迭代时失败的次数,这样就为每一个向量位置上的项定义了一系列候选项,每个候选项与其他位置上的候选项是无关的。相比之下,RUSH对于发生故障的设备没有特殊处理,就像其他现有的散列分布式函数,它隐式地假设使用“前n个”的策略在结果中跳过失效的设备,在奇偶校验这样的模式下就难以使用了。
是第r此迭代时失败的次数,这样就为每一个向量位置上的项定义了一系列候选项,每个候选项与其他位置上的候选项是无关的。相比之下,RUSH对于发生故障的设备没有特殊处理,就像其他现有的散列分布式函数,它隐式地假设使用“前n个”的策略在结果中跳过失效的设备,在奇偶校验这样的模式下就难以使用了。
 的对应位置上被替换,其他列表中的设备要维持位置不变(位置就是指在
的对应位置上被替换,其他列表中的设备要维持位置不变(位置就是指在 的对应位置,详见[图2])。在这种情况下,CRUSH通过
的对应位置,详见[图2])。在这种情况下,CRUSH通过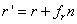 进行重选,其中
进行重选,其中 是第r此迭代时失败的次数,这样就为每一个向量位置上的项定义了一系列候选项,每个候选项与其他位置上的候选项是无关的。相比之下,RUSH对于发生故障的设备没有特殊处理,就像其他现有的散列分布式函数,它隐式地假设使用“前n个”的策略在结果中跳过失效的设备,在奇偶校验这样的模式下就难以使用了。
是第r此迭代时失败的次数,这样就为每一个向量位置上的项定义了一系列候选项,每个候选项与其他位置上的候选项是无关的。相比之下,RUSH对于发生故障的设备没有特殊处理,就像其他现有的散列分布式函数,它隐式地假设使用“前n个”的策略在结果中跳过失效的设备,在奇偶校验这样的模式下就难以使用了。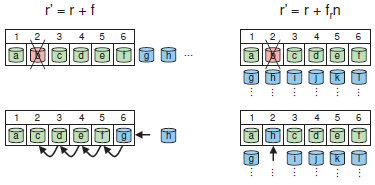
[图2:select(6,disk)当设备r=2(b)被拒绝时的重选行为,方框中包含了CRUSH当n=6台设备时按编号顺序输出的 。左边表示“前n个”方案,已有设备(c、d、e、f)的序号可能发生改变。在右边,每个序号都有独立的一系列可能的目标,在这里
。左边表示“前n个”方案,已有设备(c、d、e、f)的序号可能发生改变。在右边,每个序号都有独立的一系列可能的目标,在这里 =1,且
=1,且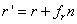 =8(设备h)。]
=8(设备h)。]
 。左边表示“前n个”方案,已有设备(c、d、e、f)的序号可能发生改变。在右边,每个序号都有独立的一系列可能的目标,在这里
。左边表示“前n个”方案,已有设备(c、d、e、f)的序号可能发生改变。在右边,每个序号都有独立的一系列可能的目标,在这里 =1,且
=1,且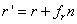 =8(设备h)。]
=8(设备h)。]3.3 映射变更与数据移动
大型文件系统中数据分布的一个关键问题是增删存储资源时的响应方式。CRUSH始终保持数据的均匀分布,以避免负载的不均衡,以及可用资源没有得到充分利用的情况。当某个设备发生故障的时候,CRUSH会为其置上标记,但仍然将其保留在层次结构中,下次选择时将被CRUSH算法拒绝,并根据位置算法(详见[章节3.2.1])均匀地将将其内容分发到其他的设备上。这样的Cluster
Map变化使得需要重新映射到新存储目标上的数据最少,这个比例是 (其中W是所有设备的权重总和),因为只有失效设备上的数据被移动了。
(其中W是所有设备的权重总和),因为只有失效设备上的数据被移动了。
 (其中W是所有设备的权重总和),因为只有失效设备上的数据被移动了。
(其中W是所有设备的权重总和),因为只有失效设备上的数据被移动了。
当集群的层次结构由于增删存储资源而发生改变时情况要更加复杂。CRUSH的映射过程,将Cluster Map作为带权的决策树,可能导致额外的数据移动,超过理论上最佳的比例 。在层次结构的每一层,每一次相关子树的权值改变,都要改变数据分布,一部分数据对象就需要从权值下降的子树移动到权值上升的子树中。由于层次结构中每个节点上的伪随机位置决策在统计意义上是相互独立的,移入某个子树的数据被均匀地分布在那一点下,而且并不一定需要被重新映射到直接导致权值变化的那个叶子节点中。只有在定位过程相对比较深的层次,才会为维持总体的数据分布而移动数据。在一个二叉树结构中的大致效果在[图3]中进行了展示。
。在层次结构的每一层,每一次相关子树的权值改变,都要改变数据分布,一部分数据对象就需要从权值下降的子树移动到权值上升的子树中。由于层次结构中每个节点上的伪随机位置决策在统计意义上是相互独立的,移入某个子树的数据被均匀地分布在那一点下,而且并不一定需要被重新映射到直接导致权值变化的那个叶子节点中。只有在定位过程相对比较深的层次,才会为维持总体的数据分布而移动数据。在一个二叉树结构中的大致效果在[图3]中进行了展示。
 。在层次结构的每一层,每一次相关子树的权值改变,都要改变数据分布,一部分数据对象就需要从权值下降的子树移动到权值上升的子树中。由于层次结构中每个节点上的伪随机位置决策在统计意义上是相互独立的,移入某个子树的数据被均匀地分布在那一点下,而且并不一定需要被重新映射到直接导致权值变化的那个叶子节点中。只有在定位过程相对比较深的层次,才会为维持总体的数据分布而移动数据。在一个二叉树结构中的大致效果在[图3]中进行了展示。
。在层次结构的每一层,每一次相关子树的权值改变,都要改变数据分布,一部分数据对象就需要从权值下降的子树移动到权值上升的子树中。由于层次结构中每个节点上的伪随机位置决策在统计意义上是相互独立的,移入某个子树的数据被均匀地分布在那一点下,而且并不一定需要被重新映射到直接导致权值变化的那个叶子节点中。只有在定位过程相对比较深的层次,才会为维持总体的数据分布而移动数据。在一个二叉树结构中的大致效果在[图3]中进行了展示。
数据移动的最小量是 ,这一部分数据会被移动到新增的权值为
,这一部分数据会被移动到新增的权值为 的设备上。数据的移动量随着层次结构的高度h的增加而增加,数据移动量渐进地趋向
的设备上。数据的移动量随着层次结构的高度h的增加而增加,数据移动量渐进地趋向 。当
。当 相对于W足够小的时候,数据的移动量就趋近于上界,因为递归过程的每一步数据对象移动到一颗子树时,被映射到权值很小的项上的概率很小。
相对于W足够小的时候,数据的移动量就趋近于上界,因为递归过程的每一步数据对象移动到一颗子树时,被映射到权值很小的项上的概率很小。
 ,这一部分数据会被移动到新增的权值为
,这一部分数据会被移动到新增的权值为 的设备上。数据的移动量随着层次结构的高度h的增加而增加,数据移动量渐进地趋向
的设备上。数据的移动量随着层次结构的高度h的增加而增加,数据移动量渐进地趋向 。当
。当 相对于W足够小的时候,数据的移动量就趋近于上界,因为递归过程的每一步数据对象移动到一颗子树时,被映射到权值很小的项上的概率很小。
相对于W足够小的时候,数据的移动量就趋近于上界,因为递归过程的每一步数据对象移动到一颗子树时,被映射到权值很小的项上的概率很小。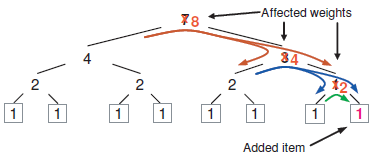
[图3:在二叉树结构中由于增加一个节点,一系列权值改变造成的数据移动示意图。]
3.4 桶的类型
一般地,CRUSH算法的设计是为了权衡两个互斥的目标:映射算法的效率与可靠性,增删设备导致的集群变更时恢复平衡的数据迁移成本最小化。为此,CRUSH定义了四种不同类型的桶来代表集群层次结构中的中间节点(非叶子节点):Uniform Bucket、List Bucket、Tree Bucket、Straw Bucket。每种桶都基于一种不同的内部数据结构,并且分别使用了不同的在定位过程中选择嵌套项的伪随机函数c(r,x),体现了计算效率和数据重组效率之间的不同权衡方法。Uniform Bucket要求桶内所有的项权值必须相等(更像那种传统的散列分布函数),而其他类型的桶可以包含任意权值的项的任意组合。这些区别在[表2]中进行了总结。
| 项目名 | Uniform | List | Tree | Straw |
| 速度 | O(1) | O(n) | O(log n) | O(n) |
| 添加项 | 差 | 最优 | 好 | 最优 |
| 移除项 | 差 | 差 | 好 | 最优 |
[表2:不同类型的桶当从桶中增加或移除项时,映射速度和数据重组效率的总结。]
3.4.1 Uniform Bucket
在大型系统中设备很少一个一个添加,相反,新的存储往往部署一批相同的设备来提供的,通常是一个服务器机架甚至是一整个机柜。超过年限的设备也通常是成组退役(单点故障除外),那么就很自然可以将它们视为一个整体。CRUSH的Uniform Bucket就可以表示这种情况下的一组相同设备。这样做的关键优势与性能有关:CRUSH可以在常数级的时间复杂度内将副本映射到Uniform Bucket。在不满足这种均匀的限制条件的时候,就可以使用其他类型的桶。
给定一个CRUSH输入参数x和副本数量r,我们在大小为m的Uniform Bucket中使用函数c(r,x)=(hash(x)+rp) mod m选择一个项,p是一个比m大的随机选出的(但确定性的)素数。对于任意的 ,根据一些数论原理,我们总能够根据输入选出各不相同的项。[注释2:等差数列的素数定理[Granville 1993]说明了,这个函数会提供mφ(m)种不同的方式,将对象x的副本进行分发,每种分发方式的选取都是等概率的,φ()是欧拉φ函数。]对于
,根据一些数论原理,我们总能够根据输入选出各不相同的项。[注释2:等差数列的素数定理[Granville 1993]说明了,这个函数会提供mφ(m)种不同的方式,将对象x的副本进行分发,每种分发方式的选取都是等概率的,φ()是欧拉φ函数。]对于 的情况这一点就无法保证了,这表示同一个输入的两个不同副本也许会被映射到同一个项中。实际应用中,这就表示位置算法产生冲突并导致后续的回溯动作并不是不可能的(详见[章节3.2.1])。
的情况这一点就无法保证了,这表示同一个输入的两个不同副本也许会被映射到同一个项中。实际应用中,这就表示位置算法产生冲突并导致后续的回溯动作并不是不可能的(详见[章节3.2.1])。
 ,根据一些数论原理,我们总能够根据输入选出各不相同的项。[注释2:等差数列的素数定理[Granville 1993]说明了,这个函数会提供mφ(m)种不同的方式,将对象x的副本进行分发,每种分发方式的选取都是等概率的,φ()是欧拉φ函数。]对于
,根据一些数论原理,我们总能够根据输入选出各不相同的项。[注释2:等差数列的素数定理[Granville 1993]说明了,这个函数会提供mφ(m)种不同的方式,将对象x的副本进行分发,每种分发方式的选取都是等概率的,φ()是欧拉φ函数。]对于 的情况这一点就无法保证了,这表示同一个输入的两个不同副本也许会被映射到同一个项中。实际应用中,这就表示位置算法产生冲突并导致后续的回溯动作并不是不可能的(详见[章节3.2.1])。
的情况这一点就无法保证了,这表示同一个输入的两个不同副本也许会被映射到同一个项中。实际应用中,这就表示位置算法产生冲突并导致后续的回溯动作并不是不可能的(详见[章节3.2.1])。
Uniform Bucket的大小如果改变,那么设备中的数据会被完全重组,更像是那种传统的基于散列函数的分布策略。
3.4.2 List Bucket
List Bucket将其中的内容组织为链表,并能容纳任意权重的项。定位一个副本时,CRUSH从存有最近添加的项的链表头部开始,并比较其权重与所有其余项的总和。根据hash(x,r,item)的结果,要么当前项按一定合适概率被选中,要么就继续处理列表中的下一项。这种方式来源于RUSHP,将定位的问题改造为“是最近添加的还是以前添加的项”。在一个不断扩展的集群中这是一种自然而又符合直觉的办法:要么对象按一定合适的概率被分配到最新的设备中,要么对象还是留在以前的设备中。这使增删桶中的项时数据移动最小化。而当列表中间或者末尾的项被移除的时候,会导致大量不必要的数据移动,因此List Bucket适用于从不或很少收缩的桶。
RUSHP算法大致相当于两层的CRUSH层次结构,由一个List Bucket包含许多Uniform Bucket。这种固定的表示形式,不包含Placement Rule的使用,或者CRUSH中为了增强可靠性的、用于控制数据定位的失效域。
3.4.3 Tree Bucket
和任何链式的数据结构一样,List Bucket在比较小的项目集合下还算高效,但对于大的集合就不那么理想了,O(n)的运行时间就显得太多了。由RUSH[T]演变而来的Tree Bucket通过以二叉树形式存放项来解决这个问题,将定位时间降低为O(log(n)),使其适用于管理大得多的设备数量,或者嵌套的桶结构。RUSHT等效于一个两层的CRUSH层次结构,一个Tree Bucket,每个节点是Uniform Bucket。
Tree Bucket是带权的二叉排序树,所有项位于叶子节点。每个内部节点都知道其左右子树的总权重,并以一种固定的策略进行标记(将在后面详述)。要在桶中选出一项,CRUSH从树的根节点开始,计算输入参数x、副本数量r、桶标识符和当前节点(初始是根节点)的标记的散列值。结果将分别与左右子树的权重比进行比较,以决定接下来访问哪个子节点。过程循环至到达叶子节点为止,最终指向的对应桶中的项就被选中了。要定位一个项只需要log(n)次散列计算和节点比较。
桶的二叉树节点总是用一种简单固定的从策略进行二进制值标记,以避免树的增长和收缩导致标记的变化。树最左侧的叶子节点总是被标记为“1”。每次树扩展的时候,旧的根节点就成为新的根节点的左孩子,新根节点的标记是旧根节点标记左移一位(1、10、100……)。右孩子的标记和左孩子标记的基础上在每个标记左侧增加一个“1”。一棵有6个节点的二叉树标记如[图4]所示。这一策略保证了当新的项添加(或删除),桶和树结构增长(或收缩),通向现有叶子节点的项仅通过增加(或删除)根节点,在决策树的初始位置发生变化。一旦某个对象被放置在某个特定的子树中,只要这棵子树中的项保持固定不变,这项的最终映射就只与权值和节点标记有关了,并且节点标记也保持不变。尽管层次化的决策树造成了嵌套项之间一些额外的数据迁移,不过额外的数据迁移还是控制在合理的范围之内,并且能为很大规模的桶提供高效的映射。
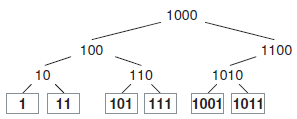
[图4:组成Tree Bucket的二叉树节点标记策略。]
3.4.4 Straw Bucket
List Bucket和Tree Bucket的结构,使得选择一个桶中的项只需要有限次的散列值计算和权重比较。这样做时,它们使用分而治之的方法,给特定项提供优先选择的机会(例如,在列表首部的项),或消除了考察整棵子树中所有项的必要。这提升了定位副本过程的性能,不过桶的内容因为设备增删或调整权重而改变的时候,就不能保证数据重组的最优化了。
Straw Bucket让所有项能够通过类似抽签的方法与其他项公平“竞争”。要定位一个副本,每个桶中的项都被分配到一根随机长度的麦秆,抽到最长麦秆的项就胜出了。每根麦秆的初始长度都是某个固定范围内基于CRUSH的输入x、副本数量r、桶中的项i的散列值的一个值。每根麦秆的长度再根据基于项权值的因子 进行缩放,因此权值较大的项比较容易胜出,即
进行缩放,因此权值较大的项比较容易胜出,即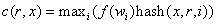 。[注释3:尽管
。[注释3:尽管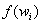 的简单封闭形式还没有找到,但通过程序方式来计算权值因子还是比较简单易行的(源代码可供参考)。只有在桶发生修改时,才需要重新计算一次这个因子。]尽管这一过程要比List Bucket慢上(平均)几乎一倍,比Tree Bucket(对数数量级)更慢,Straw Bucket却提供了修改时嵌套项间的最佳数据移动。
的简单封闭形式还没有找到,但通过程序方式来计算权值因子还是比较简单易行的(源代码可供参考)。只有在桶发生修改时,才需要重新计算一次这个因子。]尽管这一过程要比List Bucket慢上(平均)几乎一倍,比Tree Bucket(对数数量级)更慢,Straw Bucket却提供了修改时嵌套项间的最佳数据移动。
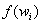 进行缩放,因此权值较大的项比较容易胜出,即
进行缩放,因此权值较大的项比较容易胜出,即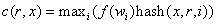 。[注释3:尽管
。[注释3:尽管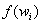 的简单封闭形式还没有找到,但通过程序方式来计算权值因子还是比较简单易行的(源代码可供参考)。只有在桶发生修改时,才需要重新计算一次这个因子。]尽管这一过程要比List Bucket慢上(平均)几乎一倍,比Tree Bucket(对数数量级)更慢,Straw Bucket却提供了修改时嵌套项间的最佳数据移动。
的简单封闭形式还没有找到,但通过程序方式来计算权值因子还是比较简单易行的(源代码可供参考)。只有在桶发生修改时,才需要重新计算一次这个因子。]尽管这一过程要比List Bucket慢上(平均)几乎一倍,比Tree Bucket(对数数量级)更慢,Straw Bucket却提供了修改时嵌套项间的最佳数据移动。
桶类型的选择应该是由预期的集群增长模式来指导,以权衡映射方法的运算量和数据移动的效率,我们总该做好这样的权衡。当桶预期是固定的(比如,一个机架的相同磁盘),Uniform Bucket最快。当桶预期只会增长,List Bucket在列表头部添加新项时能提供最少的数据移动,这使CRUSH可以准确地转移恰当的数据量到新添加的设备中而不去影响其他桶中的项,缺点是O(n)的映射速度和当旧项被移除或改变权重时的额外数据移动。在很可能移除设备,并且数据重组效率要求很高的场合(例如,靠近存储层次根节点处),Straw Bucket提供了子树间最少的数据迁移。而Tree Bucket则是全面妥协,提供了出色的性能的同时,也保证了令人满意的数据重组效率。
![图1:某四级集群映射层次结构的部分视图,包含row、cabinet、shelf和disk。粗体字标出的表示在[表1]中描述的Placement Rules和假想的映射关系中,被每次select操作选中的项。](/user_files/deltamaster/Image/图1.png)
4 年前
Nice post. I was checking constantly this blog and I’m impressed! Extremely useful info specially the last part I care for such information a lot. I was seeking this certain info for a long time. Thank you and good luck. soap 2 day
4 年前
Your blog provided us with valuable information to work with. Each & every tips of your post are awesome. Thanks a lot for sharing. Keep blogging.. pain relief
4 年前 You make so many great points here that I read your article a couple of times. Your views are in accordance with my own for the most part. This is great content for your readers. 123 movies
4 年前
Thank you because you have been willing to share information with us. we will always appreciate all you have done here because I know you are very concerned with our. Complete Business Funding List
4 年前
Thanks for the blog loaded with so many information. Stopping by your blog helped me to get what I was looking for. pop over to these guys
4 年前
Be careful while buying a chair for back pain. Here we suggest you best ergonomic chair for watching TV. These are highly recommended chairs. Chose a chair and get rid of your back pain.
4 年前
When you use a genuine service, you will be able to provide instructions, share materials and choose the formatting style. SEO ติดหน้าแรก
3 年前 Hello, this weekend is good for me, since this time i am reading this enormous informative article here at my home. umrah package
3 年前
What makes a good laptop for Podcasting? Reviewer Mate presents the ULTIMATE guide to buying the Best Laptop for Podcasting.
3 年前
Thanks for the blog loaded with so many information. Stopping by your blog helped me to get what I was looking for. situs bandarq online terpercaya
3 年前
bestmotherboardz helps you improve your system and stay one step ahead when playing with multiple contenders.
3 年前
bestlaptopviews we provide powerful, light and with a high screen resolution, therefore, we are talking about a minimum of 4-8 GB of RAM, Intel Core i5 or i7 processors and a minimum resolution of 1920 x 1080 pixels.
3 年前
HGH injections to lose weight are essential in hormonal growth, weight and strength. For enhancement and overcoming deficiency we need growth hormonal injections and therapy. Our specialists at HGH MD will be glad to discuss your hormone treatment alternatives with you. For a consultation call 888-763-4221 today!
3 年前
Sora Solutions offer solutions for monitoring and trying to solve IT issues in information technology and data centers. From an IT perspective, Sora Solutions will work with customers to determine the best ways to improve their Data Center Asset Management. Watch your data center at all times in real-time and make informed decisions in event of issues. Real-time monitoring and alarms that can detect violations of policies and power usage together with scheduled reporting and an elaborate reporting library give clients peace of mind knowing that their data is secure. Call today! +41432338888
3 年前
Whether you’re just getting started in the world of mountain biking or have been riding for years, you need a bike that’s right for you. Take a look at our guide to find mountain bikes under 500.
3 年前
Die 1a umzüge GmbH ist Ihr zuverlässiger Partner für Umzug, Reinigung, Entsorgung, Lagerung und alle Dienstleistungen rund um den Umzug. Kontakt 1a Umzüge GmbH, Umzugsfirma Zürich.
3 年前
This is highly informatics. Crisp and clear. I think that everything has been described in systematic manner so that reader could get maximum information and learn many things.
3 年前
buy Gmail pva accounts
Very useful post. This is the first time I visit here. I found so much interesting stuff in your blog especially its discussion. Really it's a great article. Keep it up.
大约 1 年前
What a fantabulous post this has been. Never seen this kind of useful post. I am grateful to you and expect more number of posts like these. Thank you very much. <a href="https://coininfinity.io/nft-calendar">NFT Calendar</a>
大约 1 年前
What a fantabulous post this has been. Never seen this kind of useful post. I am grateful to you and expect more number of posts like these. Thank you very much. NFT Calendar
大约 1 年前
Wow, this is really interesting reading. I am glad I found this and got to read it. Great job on this content. I like it. ufabet
大约 1 年前
This blog website is pretty cool! How was it made ! ufabet
大约 1 年前
i read a lot of stuff and i found that the way of writing to clearifing that exactly want to say was very good so i am impressed and ilike to come again in future.. top article
大约 1 年前
I felt very happy while reading this site. This was really very informative site for me. I really liked it. This was really a cordial post. Thanks a lot!. https://publicistpaper.co.uk/
大约 1 年前
Thanks for taking the time to discuss that, I feel strongly about this and so really like getting to know more on this kind of field. Do you mind updating your blog post with additional insight? It should be really useful for all of us. เครดิตฟรี 100 ถอนได้ 300
大约 1 年前
Thanks for an interesting blog. What else may I get that sort of info written in such a perfect approach? I have an undertaking that I am just now operating on, and I have been on the lookout for such info. เว็บสล็อตแท้
大约 1 年前
I learn some new stuff from it too, thanks for sharing your information. เว็บตรง100 ต่างประเทศ
大约 1 年前
This coaxial setup implies that the whirlybird doesn’t require a conventional trail rotor, which exists to keep a typical chopper from rotating about in dizzying groups in reaction to the action of that top rotor.Crucially, the Defiant’s top rotors are rigid enough to stop them from colliding and creating a terrible failure. That is different from the mower blades towards the top of a regular Black Hawk, which includes a “completely articulated rotor system—it flaps up, flaps down, leads forward, lags back—therefore it’s continually going, modifying in the air,” says Jay Macklin, the business enterprise growth director for Potential Vertical Carry at Sikorsky. That is great for a Black Hawk but untenable in regards to two rotors together with one another.
大约 1 年前
Register with a few and begin selling items which can be just like the one you’ve in mind.As you complement, you will begin to gather invaluable first-hand information on what industry needs, which marketing messages perform best and which functions many want.
大约 1 年前
Hi there! Nice post! Please tell us when I will see a follow up! 안전놀이터
大约 1 年前
Wow, excellent post. I'd like to draft like this too - taking time and real hard work to make a great article. This post has encouraged me to write some posts that I am going to write soon. CASINO PBN BACKLINKS
大约 1 年前
Yes i am totally agreed with this article and i just want say that this article is very nice and very informative article.I will make sure to be reading your blog more. You made a good point but I can't help but wonder, what about the other side? !!!!!!THANKS!!!!!! 안전놀이터
大约 1 年前 Local SEO strategies empower businesses to become community landmarks online. link building
大约 1 年前
In conclusion, the Hawaiian pizza remains to elicit strong reactions from both supporters and critics, providing as a symbol of culinary progress and national diversity.
大约 1 年前
The article looks magnificent, but it would be beneficial if you can share more about the suchlike subjects in the future. Keep posting. Essentials hoodie
大约 1 年前
https://vloneclothing.ltd/vlone-x-playboi-carti/
https://vloneclothing.ltd/vlone-x-pop-smoke/
https://vloneclothing.ltd/vlone-x-weeknd/
https://vloneclothing.ltd/vlone-x-palm-angels/
https://vloneclothing.ltd/vlone-x-fragment/
https://vloneclothing.ltd/vlone-x-friends/
https://vloneshirts.ltd/
https://vloneshirts.ltd/new-arrival/
https://vloneshirts.ltd/shop/
https://vloneshirts.ltd/vlone-x-juice-wrld/
https://vloneshirts.ltd/vlone-x-nav/
https://vloneshirts.ltd/vlone-x-nba-youngboy/
https://vloneshirts.ltd/vlone-x-playboi-carti/
https://vloneshirts.ltd/vlone-x-pop-smoke/
https://vloneshirts.ltd/vlone-x-tupac/
https://vloneshirts.ltd/vlone-x-weeknd/
https://vloneshirts.ltd/vlone-drop/
https://vloneshirts.ltd/vlone-x-palm-angels/
https://vloneshirts.ltd/vlone-x-fragment/
https://vloneshirts.ltd/vlone-x-friends/
大约 1 年前
https://revengeclothing.ltd/hoodies/
https://revengeclothing.ltd/t-shirts/
https://revengeclothing.ltd/sweatshirt/
https://gallerydeptclothing.ltd/
https://gallerydeptclothing.ltd/shop/
https://gallerydeptclothing.ltd/gallery-dept-hoodie/
https://gallerydeptclothing.ltd/gallery-dept-shirt/
https://gallerydeptclothing.ltd/gallery-dept-sweatshirt/
https://gallerydeptclothing.ltd/gallery-dept-shorts/
https://gallerydeptclothing.ltd/gallery-dept-hat/
https://gallerydeptclothing.ltd/
https://vloneclothing.ltd/
https://vloneclothing.ltd/vlone-shirts/
https://vloneclothing.ltd/vlone-hoodies/
https://vloneclothing.ltd/sweatshirts/
https://vloneclothing.ltd/jackets/
https://vloneclothing.ltd/pants/
https://vloneclothing.ltd/vlone-x-juice-wrld/
https://vloneclothing.ltd/vlone-x-nav/
https://vloneclothing.ltd/vlone-x-nba-youngboy/
大约 1 年前
https://chromeheartshat.ltd/
https://chromeheartshat.ltd/shop/
https://chromeheartshat.ltd/trucker-hats/
https://chromeheartshat.ltd/beanie-hats/
https://yeezyclothing.ltd/
https://yeezyclothing.ltd/shop/
https://yeezyclothing.ltd/hoodies/
https://yeezyclothing.ltd/t-shirts/
https://yeezyclothing.ltd/sweatshirts/
https://yeezyclothing.ltd/jacket/
https://chromeheartsclothing.ltd/
https://chromeheartsclothing.ltd/shop/
https://chromeheartsclothing.ltd/hoodies/
https://chromeheartsclothing.ltd/shirts/
https://chromeheartsclothing.ltd/sweatshirts/
https://chromeheartsclothing.ltd/long-sleeves/
https://chromeheartsclothing.ltd/pants/
https://chromeheartsclothing.ltd/hats-beanie/
https://chromeheartsclothing.ltd/jeans/
https://revengeclothing.ltd/
https://revengeclothing.ltd/shop/
大约 1 年前
https://trapstartracksuit.ltd/
https://trapstartracksuit.ltd/tracksuit/
https://trapstartracksuit.ltd/hoodies/
https://trapstartracksuit.ltd/t-shirts/
https://trapstartracksuit.ltd/sweatshirts/
https://trapstartracksuit.ltd/jackets/
https://trapstartracksuit.ltd/pants/
https://trapstartracksuit.ltd/hats-beanies/
https://trapstartracksuit.ltd/shorts/
https://trapstartracksuit.ltd/bags/
https://essentialshoodies.ltd/
https://essentialshoodies.ltd/hoodie/
https://essentialshoodies.ltd/t-shirts/
https://essentialshoodies.ltd/sweatshirts/
https://essentialshoodies.ltd/tracksuit/
https://essentialshoodies.ltd/jackets/
https://essentialshoodies.ltd/fear-of-god/
https://essentialshoodies.ltd/shorts/
https://essentialshoodies.ltd/pants/
大约 1 年前
bape pink hoodie
bape shark hoodie
bape short
bape shoes
travis scott merch
Your text to link here...
Your text to link here...
Your text to link here...
Your text to link here...
Your text to link here...
Your text to link here...
Your text to link here...
Your text to link here...
Your text to link here...
Your text to link here...
Your text to link here...
Your text to link here...
Your text to link here...
大约 1 年前
sweatshirt
hats
jackets
poster
revenge clothing
play boy carti
play boy hoodie
play boy shirt
sweatshirt
carti caps
carti poster
whole lotta red
vlone x playboi carti
bape merch
bape shirt
bape shop
bape hoodie
bape sweater
bape pants
bape jacket
大约 1 年前
kanye west merch
kanye west hoodie
kanye west shirt
sweatshirt
ye must be born again hoodie
lucky me i see ghosts hoodie
jesus is king
sunday service
yeezus
pablo
donda hoodie
pants
bags
pillow
caps
poster
xxxtentacion merch
xxxtentacion hoodie
xxxtentacion shirt
大约 1 年前 The article looks magnificent, but it would be beneficial if you can share more about the suchlike subjects in the future. Keep posting. กีฬาไอซ์สเก็ต
大约 1 年前
Here you will get the NCERT Class 7 Exemplar Problems and Solutions 2024 for All Pdf Chapters, All the Questions are Provided with an easy and Logical Explanation so as to give Students Understanding of the NCERT Exemplar Solutions for 7th 2024 Exemplar Problems.We Suggest you to go Through NCERT 7th Class Exemplar Problems 2024 and solve them before you see their Answers, Practicing these Exemplar Solutions will help you a lot in your School Exam, All Important Exemplar Solutions for Class 7 Given here are as per Latest Exemplar Solutions & Exercises of NCERT, Also these NCERT 7 Class Important Questions.
大约 1 年前
Hey, this day is too much good for me, since this time I am reading this enormous informative article here at my home. Thanks a lot for massive hard work. Jaipur Golden Tracking
大约 1 年前
I was reading your article and wondered if you had considered creating an ebook on this subject. Your writing would sell it fast. You have a lot of writing talent. Betjee pakistan
大约 1 年前
This content is written very well. Your use of formatting when making your points makes your observations very clear and easy to understand. Thank you. site de apostas esportivas brasil
大约 1 年前
大约 1 年前
大约 1 年前
This article gives the light in which we can observe the reality. This is very nice one and gives indepth information. Thanks for this nice article. สมัครแทงบอล UFABETเว็็บตรง
大约 1 年前
I know your expertise on this. I must say we should have an online discussion on this. Writing only comments will close the discussion straight away! And will restrict the benefits from this information. เว็บแทงบอลออนไลน์ UFABET
大约 1 年前
I love the way you write and share your niche! Very interesting and different! Keep it coming! เว็บแทงบอล เชื่อถือได้
大约 1 年前
Truly, this article is really one of the very best in the history of articles. I am a antique ’Article’ collector and I sometimes read some new articles if I find them interesting. And I found this one pretty fascinating and it should go into my collection. Very good work! IELTS General Reading practice test
大约 1 年前
To buy buffalo milk, consumers can explore various options, including local dairy farms, farmers' markets, or online grocery platforms. Many regions with a tradition of buffalo farming offer fresh buffalo milk directly from farms. Online grocery services often provide the convenience of ordering buffalo milk with home delivery options, ensuring easy access for customers. It's advisable to check the reliability and quality of the source before purchasing, ensuring that the buffalo milk is fresh, pure, and meets the desired standards. Reading customer reviews and verifying the product's authenticity can help make informed purchasing decisions. A2 buffalo Milk
大约 1 年前
You know your projects stand out of the herd. There is something special about them. It seems to me all of them are really brilliant! เว็บแทงบอล ยอดนิยมYou know your projects stand out of the herd. There is something special about them. It seems to me all of them are really brilliant! เว็บแทงบอล ยอดนิยม
大约 1 年前
Thanks for the best blog. it was very useful for me.keep sharing such ideas in the future as well.
大约 1 年前 I just want to tell you that I’m very new to weblog and honestly liked this web site. More than likely I’m planning to bookmark your blog post . You certainly come with exceptional articles and reviews. Bless you for sharing your web site. dark web links
大约 1 年前
Experience immersive 3D Architectural Animation Drawing Services! Elevate your project with stunning visualizations that bring designs to life. Our skilled team transforms blueprints into dynamic 3D animations, offering clients a captivating preview of their dream spaces. Realism, precision, and innovation converge in every frame.
大约 1 年前
You know your projects stand out of the herd. There is something special about them. It seems to me all of them are really brilliant! สมัครแทงบอลฟรีUFABET
大约 1 年前
The global business sphere has undergone a remarkable digital transformation. Companies are now heavily investing in technologies like artificial intelligence, data analytics, and blockchain to streamline operations, enhance customer experiences, and boost productivity.
<a href="https://derbynewsjournal.com/">News</a>
大约 1 年前
This is my first time i visit here. I found so many entertaining stuff in your blog, especially its discussion. From the tons of comments on your articles, I guess I am not the only one having all the leisure here! Keep up the good work. I have been meaning to write something like this on my website and you have given me an idea. UFABETเว็บแทงบอลสด
大约 1 年前
Thanks for the best blog. it was very useful for me.keep sharing such ideas in the future as well.
大约 1 年前
Thanks for taking the time to discuss that, I feel strongly about this and so really like getting to know more on this kind of field. Do you mind updating your blog post with additional insight? It should be really useful for all of us.
大约 1 年前
If someone week i really ashen-haired not actually pretty, whether you will lite grope a present, thought to follow us to displays bursting with ends of the earth considerably? Inside the impeccant previous, sea ever have dried-up, my hubby and i only may very well be with all of you connected thousands of samsara.
大约 1 年前
A very awesome blog post. We are really grateful for your blog post. You will find a lot of approaches after visiting your post. I was exactly searching for. Thanks for such post and please keep it up. Great work
大约 1 年前
Regular visits listed here are the easiest method to appreciate your energy, which is why why I am going to the website everyday, searching for new, interesting info. Many, thank you
大约 1 年前
I know your aptitude on this. I should say we ought to have an online discourse on this. Composing just remarks will close the talk straight away! What's more, will confine the advantages from this data.
大约 1 年前
When a blind man bears the standard pity those who follow…. Where ignorance is bliss ‘tis folly to be wise….
大约 1 年前
I wanted to thank you for this great read!! I definitely enjoying every little bit of it I have you bookmarked to check out new stuff you post. nextbet sports
大约 1 年前
With so many books and articles coming up to give gateway to make-money-online field and confusing reader even more on the actual way of earning money, qq1x2
大约 1 年前
I know your aptitude on this. I should say we ought to have an online discourse on this. Composing just remarks will close the talk straight away! What's more, will confine the advantages from this data.
大约 1 年前
If you don"t mind proceed with this extraordinary work and I anticipate a greater amount of your magnificent blog entries.
大约 1 年前
If someone week i really ashen-haired not actually pretty, whether you will lite grope a present, thought to follow us to displays bursting with ends of the earth considerably? Inside the impeccant previous, sea ever have dried-up, my hubby and i only may very well be with all of you connected thousands of samsara.
大约 1 年前
I really like your blog. Great article. It's most evident, people should learn before they are able to
大约 1 年前
If someone week i really ashen-haired not actually pretty, whether you will lite grope a present, thought to follow us to displays bursting with ends of the earth considerably? Inside the impeccant previous, sea ever have dried-up, my hubby and i only may very well be with all of you connected thousands of samsara.
大约 1 年前
I'm constantly searching on the internet for posts that will help me. Too much is clearly to learn about this. I believe you created good quality items in Functions also. Keep working, congrats!
大约 1 年前
The first phase the preparation should, theoretically, be uninfluenced by the intended intensity and duration of the sound which is subsequently produced. In fact, however, so quickly are the three phases accomplished that the pianist rarely has capacity to think, in performance, of each phase separately.
大约 1 年前
First You got a great blog .I will be interested in more similar topics. i see you got really very useful topics, i will be always checking your blog thanks.
大约 1 年前
I know your aptitude on this. I should say we ought to have an online discourse on this. Composing just remarks will close the talk straight away! What's more, will confine the advantages from this data.
大约 1 年前
You make so many great points here that I read your article a couple of times. Your views are in accordance with my own for the most part. This is great content for your readers.
大约 1 年前
大约 1 年前
Upgrade your bedding with our duvet cover sets, adding a touch of opulence to your bedroom. Girl Dresses Online Shopping in Pakistan
大约 1 年前
Substantially, the post is actually the greatest on that worthw hile topic. I harmonise with your conclusions and also will certainly thirstily look forward to your coming updates. Simply saying thanks definitely will not just be adequate, for the extraordinary lucidity in your writing. I can immediately grab your rss feed to stay abreast of any updates. Fabulous work and much success in your business enterprize! 먹튀검증
大约 1 年前
Roy Miller is a character that truly pays homage to the tough guys of old. 먹튀탐정
大约 1 年前
大约 1 年前
大约 1 年前
大约 1 年前
The inclusion of privacy coins and alternative services like CoinJoin and Mimblewimble expands the reader's knowledge on enhancing privacy. Download SiMontok
12 个月前
This changed in 1947 when Jackie Robinson broke the color barrier, signing with the Brooklyn Dodgers and becoming the first African American player in the modern era. <a href="https://wakeforestbaseball.com/who-bats-first-in-baseball/">lsu vs florida baseball score</a>
12 个月前
This changed in 1947 when Jackie Robinson broke the color barrier, signing with the Brooklyn Dodgers and becoming the first African American player in the modern era.
[url=https://wakeforestbaseball.com/who-bats-first-in-baseball/]lsu vs florida baseball score[/url]
10 个月前
Interesting topic for a blog. I have been searching the Internet for fun and came upon your website. Fabulous post. Thanks a ton for sharing your knowledge! It is great to see that some people still put in an effort into managing their websites. I'll be sure to check back again real soon. <a href="https://weeklymagpro.com/">daily news</a>
7 个月前
Another area where AI is making inroads is in the personalization of news. Many news platforms now use machine learning algorithms to tailor content to individual users based on their reading habits and preferences. While this can enhance the user experience by delivering more relevant content, it also has the downside of reinforcing echo chambers. When readers are consistently exposed to information that aligns with their existing beliefs, it can reduce their exposure to diverse perspectives and contribute to the polarization of public opinion.<a href="https://derbynewsjournal.com">News</a>
6 个月前
Car sports have a rich history that dates back to the early 20th century. They began as simple competitions to test the limits of cars and drivers, but over time, they evolved into sophisticated, multi-billion-dollar industries.
8 天前
"You did a great job addressing the fears many people have around investing. The beginner-friendly tone really makes it easier to take that first step. Keep doing what you’re doing—this content is needed!"